Surrogate Indicies

Estimating Long-Term Treatment Effects With Short Term Proxies

One of the biggest challenges I’ve faced developing examples to illustrate the utility of causal inference for problems in marketing and business analytics, is the identification of scenarios for which impact can be measured immediately as a result of a particular action. Unlike, economic policies which are generally estimated over longer time periods, iterative decision made in marketing and product organizations requires immediate evaluation of causal effects. The challenge I face is not merely identifying an outcome variable with a causal relationship to an explanatory variable in a particular business context, it is rather finding an outcome variable that can easily be tied directly to business metrics, justifying rigorous investigation. It’s not particularly difficult for Amazon to estimate the minimum discount necessary to entice the purchase of a particular item, or for Tinder to estimate how much time you’ll spend on your first session, given that you found a match on your first swipe right. The dilemma I encounter is the identification of datasets that can be tied directly to measurements of long-term business impact, such as prime subscription purchases on Amazon or total screen time per user on Tinder.

To avoid wrestling with unfounded theories explaining ties between these short-term product effects and long-term business impacts, I tend to focus solely on interventions which directly affect an organization’s business line. I typically discuss UX optimizations designed to increase the possibility that a user purchases an item within a mobile app. Such metrics can easily be used to evaluate short-term impact as they can be mapped to long term business with simple arithmetic. The monetary value of a UX change that makes a customer 3 times more likely to buy a particular product is equivalent to 3, times the amount of people who bought the product before the intervention, times the average profit margin of that product.

However, answering these first order questions only investigates a narrow slice of the analytical potential of causal inference techniques. Many of the most innovative companies leveraging causal inference rapidly increase gross revenue through flywheels, within which immediate revenue generating events result in more substantial gains over a longer time horizon. Flywheels are common in businesses commodifying marketplaces or social networks, which increase in value proportionally as they accrue more users. Consider Amazon’s flywheel pictured in Figure 1. For individual products, Amazon will often provide consumers specialized discounts, which improve their customer experience but result in an immediate loss for Amazon’s bottom line. However, because Amazon’s Flywheel mechanism increases both sellers and buyers in their marketplace with an increase in user traffic, over time, the margin Amazon makes on these products may become positive, justifying the short-term loss for long term gain.

Amazon’s growth flywheel, which many credit as the primary strategy which propelled the company to its immense success today. As illustrated, Amazon’s high-quality customer experience drives traffic to their platform, which attracts more 3P sellers, further improving the site’s customer experience. Additionally, as more buyers and sellers participate on Amazon’s platform, the company can decrease their per unit cost of selling an individual good, allowing the company to decrease prices for its users, and to improve the site’s customer experience even more.

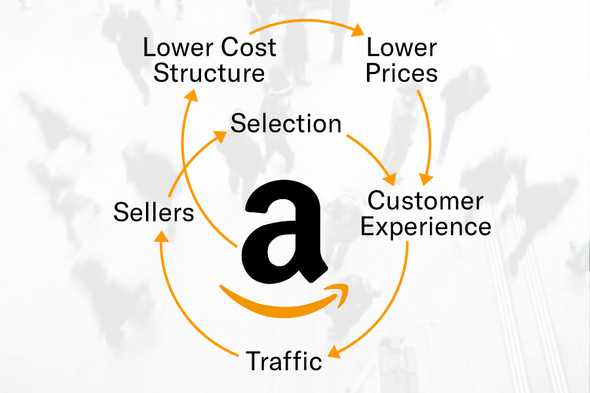
While it is often immensely valuable to estimate the effect of interventions on businesses flywheel dynamics, direct estimation often requires waiting weeks or even months for an observed fluctuation to materialize. As anyone working on an agile product cycle knows, the faster a development team can evaluate the long-term value of a particular intervention, the more efficiently they can iterate towards product improvements which maximize total revenue. In business scenarios illustrated by the example in Figure 2, businesses sacrifice a immediate losses to engender longstanding gains, so rapidly understanding the total value of a change is crucial for assessing the intervention’s profitability. Causal inference practitioners aiming to optimize key metrics can only rarely bare the costs of long-term observational studies, provoking a demand for methods enabling long-term estimation via short-term proxies.

Figure 1: Flowchart describing the impact of a discounting product feature on immediate and long-term margin of a particular product in an e-commerce marketplace.

Short Term Proxies

How can amazon immediately evaluate the total value of applied over a 6 month time period, without waiting until next year for conclusive data to materialize? More generally, how can organizations quickly evaluate the effects of interventions that occur over years, sometimes even decades? In causal inference settings for which long-term treatment effects are costly to estimate, it is common to instead evaluate short-term proxies which can be statistically proven to eventually affect observational variables of interest. For example, if Amazon were able to prove that increased demand for a particular product had a causal effect on seller volume over a longer time horizon, they could easily estimate the expected return-on-investment of a 6-month temporary discount and identify an optimal discount amount for the product accordingly.

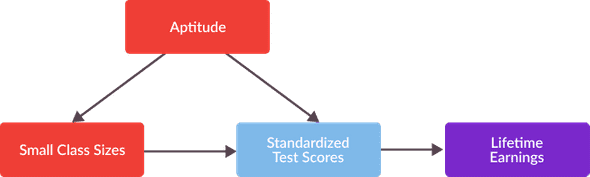
In econometrics, short-term proxies are commonly known as “statistical surrogates” for the observational variables they are hypothesized to estimate over a long time period. In observational settings, in which an analyst cannot randomly assign treatment, it is common for a variety of surrogates to intersect a causal relationship between an explanatory variable and observational variable of interest. Statistical surrogates have been used in economics and medicine for decades tracing back to Ross Prentice’s Surrogate Endpoints In Clinical Trials ¹, a seminal paper which leveraged the concept to evaluate the efficacy of various treatments for cancer prevention. Surrogates are also commonly used in the evaluation of education policies aiming to increase lifetime earnings. Since lifetime earnings are tightly correlated with the standardized test scores, an estimate causal effect of an education intervention (such as decreased class size or increased teacher’s pay) can sometimes serve as a statistical surrogate for lifetime earnings. A structural causal model illustrating this statistical relationship is presented in Figure 3.

Figure 2: Structural causal model illustrating an example of observed causal effects on between an explanatory variable of interest. class size, a candidate surrogate variable, standardized test scores, and an outcome variable lifetime earnings.

Surrogate Models

In order to leverage surrogate model analysis on a population, an analyst requires different, but related data from two groups of observed individuals $i$. From the first group, an analyst must have values of the treatment assignment explanatory variable $\color{#EF3E36}{W_i}$, their corresponding characteristics prior to treatment $\color{#EF3E36}{X_i}$ and the values of a candidate surrogate variable $\color{#7FB9E9}{S_i}$ resulting from each individuals treatment. From the second group, an analyst must have values of a candidate surrogate variable $\color{#7FB9E9}{S_i}$, their corresponding values of an outcome variable of interest $\color{#7A28CB}{Y_i}$, and pre-treatment characteristics for each individual. For example, In order to leverage a surrogate model, an analyst needs to split a set of observed individuals into two samples: an experimental ($E$) sample and an observational ($O$) sample with each sample containing $N_E$ and and $N_O$ individuals respectively. When specifying a surrogate model to estimate long-term effects, an analyst must first estimate the causal effect of treatment on a selected surrogate variable within their experimental sample. Next, they must estimate the causal effect of a selected surrogate variable on an outcome variable of interest within their observational sample. Finally, the analyst combine these two calculations, in order to generate an overarching estimation of a long-term causal effect.

Requirements For Surrogacy

How can an analyst identify which variables out of a set of “surrogate candidates” are best suited to be leveraged as statistical surrogates? In order for a particular variable to be used as a statistical surrogate, it must satisfy a pair of requirements. The first of these is un-confoundedness, a common criterion for economic program evaluation. A candidate surrogate variable is un-confounded when there are no variables affecting both the variable and treatment assignment. For example, if an analyst desired to estimate the effect of class sizes on earnings at a school where top students were more likely to be placed in smaller classes, standardized test scores would be an inadequate statistical surrogate, because a student’s academic aptitude affects both their resulting class size and their standardized test scores, thus the variable is confounded. In a previous post, I discuss confounding bias in more detail, and describe an example of how this bias could cause analysts to over-estimate the positive impact of smaller class sizes.

Figure 4: Structural causal model illustrating an example of causal effects on both an explanatory variable of interest, class size, and a candidate surrogate variable, standardized test scores, disabling standardized test scores from use as a surrogate for the long-term observational variable lifetime earnings.

The “un-confoundedness” condition for a surrogate variable is written as follows. Here, $\color{#7FB9E9}{W_i}$ represents the value of a treatment variable, $\color{#7FB9E9}{X_i}$ represents the characteristics of individual $i$ before treatment assignment, $\color{#EF3E36}{S_0, S_1}$ represents the potential outcomes of the surrogate variable, and $\color{#7FB9E9}{Y_0, Y_1}$ represents potential outcomes of the outcome variable of interest. Recall from my previous post on the potential outcome model that the subscripts 1 and 0 denote the values of a particular observed variable measured for an individual with and without treatment.

$\color{#EF3E36}{W} \color{#000000}{\perp \!\!\! \perp} \color{#7FB9E9}{S_0, S_1},\color{#7A28CB}{Y_0, Y_1} \color{#000000}{|} \color{#EF3E36}{X_i}$

In probability notation $\perp \!\!\! \perp$ means “independent”, and $|$ means “conditional”. Thus, the above equation is equivalent to the following statement: “observed individuals are assigned treatment independent of their resulting outcome and surrogate variables $\color{#7A28CB}{Y}$ and $\color{#EF3E36}{S}$, conditional on the individual’s characteristics. In the confounded class size scenario previously described, there is a characteristic of observed individuals. aptitude. that affects both class size and standardized test scores. Thus, in this scenario the un-confounedness property does not hold.

The second requirement required for a variable to be used as a surrogate is aptly named the “surrogacy condition”. In order for a potential surrogate to satisfy this condition, it must fully capture the causal link between treatment assignment, and the outcome variable of interest. When estimating the effect of smaller class sizes, on lifetime earnings, it’s not sufficient that standardized test scores merely capture a portion of the causal relationship between modest class sizes and long term income. The variable must capture the entireity of this causal relationship to be used as a surrogate. If smaller class sizes also effect the extent of social relationships that students have with their peers, and this phenomenon also has downstream effects on their lifetime earnings, then a portion of the causal link between class size and earnings is not captured merely by standardized test scores, and the surrogacy condition is not satisfied.

Figure 5: Structural causal model illustrating an example of a causal effect between class size and lifetime earnings captured by two surrogate candidates standardized test scores and social relationships, disqualifying standardized test scores from use as a surrogate for the long-term observational variable lifetime earnings.

In probability notation, the surrogacy condition can be written as follows.

$\color{#7FB9E9}{W_i} \color{#000000}{\perp \!\!\! \perp } \color{#EF3E36}{Y_i} \color{#000000}{|} \color{#7FB9E9}{S_i},\color{#7A28CB}{X_i}$

In english, the surrogacy condition states that an individual’s treatment assignment ($\color{#7FB9E9}{W_i}$), is independent of our outcome variable of interest ($\color{#7FB9E9}{Y_i}$), conditional on the surrogate candidate ($\color{#7FB9E9}{S_i}$) and the characteristics of individual $i$ prior to treatment ($\color{#7A28CB}{X_i}$). Note that if $\color{#7FB9E9}{W_i}$ is independent from $\color{#EF3E36}{Y_i}$ conditionally on $\color{#7FB9E9}{S_i}$, then there cannot be another surrogate variable $\color{#7FB9E9}{S_i'}$ representing any causal impact from the explanatory variable $\color{#EF3E36}{W_i}$ to the outcome variable $\color{#7A28CB}{Y_i}$. In the structural causal model presented in Figure 5, a second surrogate social relationships prevents our explanatory and outcome variables of interest, class size and lifetime earnings. from independence conditional on standardized test scores, and thus it cannot be used as a statistical surrogate.

The last surrogacy requirement for a variable which intercepts the causal relationship between an explanatory variable and outcome variable of interest, is comparability between observed values of the outcome variables $\color{#EF3E36}{Y_i}$ given $\color{#7FB9E9}{S_i}, \color{#7A28CB}{X_i}$ for individuals $i$ in the observational and experimental samples.

Figure 2 shows a set of short-term proxies used for a seminal paper evaluating the efficacy of the strategy for estimating the effects of regional job training programs in California.

Amazon’s Flywheel enables them subsume markets for particular products by attracting a critical mass of customers and 3rd party retailers. Thus, it is quite likely that short-term losses calculated directly from the costs of a particular discount will dwarf long-term gains of margin positive purchases once the site has cornered an online market.

Earnings from multiple quarters Get rid of “multiple” change to “simple”. Understand difference between naive short run and surrogate index