Estimating Heterogeneous Treatment Effects

In a previous blog post, I presented a methodology for quantifying causal effects by estimating average treatment effects, or the average of all effects a particular treatment (which is the another term for the proposed intervention an causal inference analyst in evaluating) has on a population of observed individuals. Estimating an average treatment effect can help an analyst understand the population level effect of a particular intervention or policy and can enable the calculation of aggregated metrics, such as an expected increase in revenue as a result of a new ad campaign or the expected result of a life-saving experimental drug. However, oftentimes an analyst isn’t interested solely in aggregated causal effects, but is rather interested in understanding the effect a policy will have on a particular individual given a set of their definitive characteristics which may or may not influence their reaction to a particular intervention. In causal inference literature, varied causal effects for individuals with varied characteristics are called heterogeneous treatment effects, and estimating these effects is a challenging problem investigated at length by academic causal inference researchers. Heterogeneous treatment effects describe how differences in the values of confounding variables for observed individuals (variables that have an effect on both the explanatory variable and outcome variable, described in my detail in my previous blog post) can change their outcomes given exposure to a treatment.

A commonly analyzed heterogeneous treatment effect estimation problem is the identification of consumers which will be influenced the most by a particular advertising campaign. In political science, heterogeneous treatment effects have been used to illuminate how different get-out-the-vote text messaging strategies have had different effects on the actions of eligible voters. One of the first applications of heterogeneous treatment effect estimation was a paper written by causal inference pioneer William Cochran, which presented a methodology for understanding the ways in which smoking can differentially affect the mortality rates of smokers of different ages, nationalities, and smoking frequencies.

Optimized Bidding For Digital Advertisements

One of the most fruitful applications of heterogeneous treatment effect estimation is within the analytics of automated bidding systems for digital advertisements. Many businesses using digital advertising to expand their customer base use automated bidding systems to purchase ads programmatically on a digital advertisement platform, such as Google Ads. These platforms provide markets with an option to automatically bid for the opportunity to show an ad to a particular user, given a provided set of their characteristics. This purchasing model is quite different then traditional advertising marketplaces, such as those used for television, billboard, and newspaper ads. In those marketplaces, a marketer pays a lump sum to purchase an advertising opportunity accessing a particular swath of the population, (ESPN fans, Highway 101 commuters, New York Times readers) and is only really concerned with how many consumers purchase their product once they are exposed to the purchased ad. On the other hand, when a marketer designs an automated bidding system to interact with digital advertising platforms, they can purchase advertising opportunities which target specific individuals most likely to subsequently convert (which means to visit the marketer’s site and take a revenue-generating action). In order to maximize the resultant profits of an advertising campaign, marketers often try to estimate the heterogeneous treatment effects of their campaigns to ensure they only purchase expensive digital advertisements that target consumers most likely to be influenced.

For example, suppose I were a marketer for a nascent budget airline brand interested in scaling up awareness of my flight offerings with an expansive digital advertising campaign. Suppose that, attracted by its reach, I choose to use Google Ads to launch my campaign. Additionally, I pay for ads “per impression”, meaning I pay a small amount every time a consumer sees one of my ads. In this scenario, if I am interested in maximizing the resulting profits from my campaign, I will want to leverage Google Ads automatic bidding features to only buy ads targeting consumers that will most likely be influenced to convert. Particularly, the causal inference task I am interested in revolves around identifying a subset of consumers for which exposure to my ad will have the greatest effect on their subsequent purchasing decisions.

Figure 2: A depiction of the process advertisers go through when using automated bidding systems to purchase an ad space displayed to an individual consumer browsing the internet. Image Credit: Match2One Blog

In order to systematically solve this causal inference problem I, predictably, will need to hypothesize a causal graph describing the causal relationship I am interested in measuring, as well as those between all variables which affect the explanatory variable and outcome variable in my causal relationship of interest. Within this causal graph, the explanatory variable I am interested in changing in order to generate revenue is:

• Exposed To Ad: Measuring whether or not an individual was exposed to an ad from my brand.

Much like the Youtube Ads Platform, discussed in my post on propensity score matching, the Google Ads Platform provides me with access to a variety of “contextual information” of internet browsing consumers, from which I can buy impressions. These variables are as follows:

• Past Behavior: Data measuring the browsing behavior of an individual consumer. This includes information such as previous engagements with my brand, generalized information about a user’s browsing history, and data detailing how often a consumer clicks through an arbitrary ad.

• Demographic Data: Data measuring the groups individual consumers belong to, such as their zip code, gender, or age.

• Psychographic Data: Data conducted from surveys measuring the interests, values, and personalities of consumers who may see my ad.

These explanatory variables all have an effect on the following outcome variable, which indirectly measures the revenue which will be generated as a result of my marketing campaign.

• Purchases Flight: Measuring whether or not an individual consumer purchases a flight from my airline within a month of seeing an ad from my campaign.

The causal graph corresponding to my digital advertising example is as follows.

Figure 3: Causal graph representing my causal relationship of interest, the effect of Exposed To Ad on Purchases Flight as well as the effects from explanatory variables affecting Exposed To Ad and Purchases Flight. Note that Past Behavior, Demographic Data, and Psychographic Data are all confounding variables. These variables have an effect on both the explanatory variable and outcome variable I am interested in.

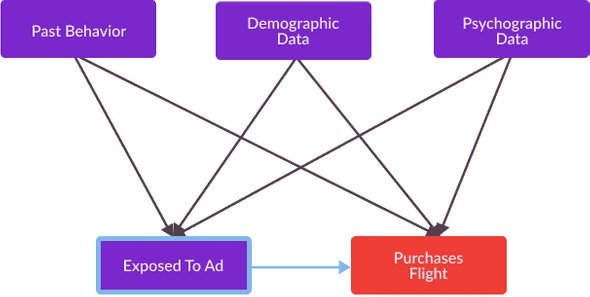
Note that Past Behavior, Demographic Data, and Psychographic Data are all confounding variables, as described in a previous blog post. These variables have an effect on both the explanatory variable and outcome variable I am interested in.

Alright, great! We drew the causal graph! What’s next? How can I use this graph and the data I have been provided to differentiate between the consumers which would be most affected by my ad and those for which an impression would not have a significant effect? Is there a way I can formalize this causal question, in order to leverage the potential outcomes framework discussed in a previous blog post?

Conditional Average Treatment Effects

The particular heterogeneous treatment effect I am interested in estimating are conditional average treatment effects (CATE), or the expected treatment effect of a particular consumer conditional on a set of explanatory variables describing them, such as Past Behavior, Demographic Data, and Psychographic Data. Formally, one can define a conditional average treatment effect as a function $\color{#7A28CB}\tau(z)$, which specifies the size of a treatment effect given a value of confounding variable $\color{#7A28CB}Z$ as follows.

$\textcolor{#7A28CB}{\tau(z)} = \mathbb{E}[\textcolor{#EF3E36}{Y_i^1 - Y_i^0}|\textcolor{#7A28CB}{Z_i = z}]$

Recall that $\color{#EF3E36}Y_i^1 - Y_i^0$ is the difference in potential outcomes from the potential outcomes model discussed in a previous blog post. In this model $\color{#EF3E36}Y_i^1$ represents an individual’s outcome given that they received treatment and $\color{#EF3E36}Y_i^0$ represents their outcome given that they did not. In probability theory, the horizontal bar ”$|$” means “conditional on”, and thus the notation above can be read as “the expected value of $\color{#EF3E36}Y_i^1 - Y_i^0$ conditional on a particular value of $\color{#7A28CB}Z_i$“.

For example, if I am interested in describing the conditional average treatment effect of Exposed To Ad ($\color{#7A28CB}A_i$) on Purchases Flight ($\color{#EF3E36}P_i$), given particular values $\color{#7A28CB}b$, $\color{#7A28CB}d$ and $\color{#7A28CB}s$ of Past Behavior ($\color{#7A28CB}B_i$), Demographic Data ($\color{#7A28CB}D_i$), and Psychographic Data ($\color{#7A28CB}S_i$) of a particular consumer I can use the following notation to describe my CATE function $\color{#7A28CB}\tau(b,d,p)$ of interest. In this notation $\color{#EF3E36}P_i^1$ the potential outcome describing whether or not individual $i$ purchases a flight given exposure to an advertisement and $\color{#EF3E36}P_i^0$ describes whether or not individual $i$ purchases a flight given no exposure to an advertisement.

$\textcolor{#7A28CB}{\tau(b,d,s)} = \mathbb{E}[\textcolor{#EF3E36}{P_i^1 - P_i^0}|\textcolor{#7A28CB}{B_i = b,D_i=d,S_i=s}]$

For my digital advertising causal inference task, I am interested in estimating the values of $\color{#7A28CB}B_i,D_i,S_i$ for which $\color{#7A28CB}\tau(z)$ will be the greatest. These are the consumers from which I can expect the most ROI on my digital advertising purchasing decisions.

For example, consider a simplified conditional average treatment effect calculation conditioning only on a single Demographic Data variable, the age of all observed individuals. Suppose that some of these consumers are under 21 and some are over 21 and that, because this is a key factor in their response to my advertisement (younger individuals with limited disposable income are unlikely to purchase a particularly expensive flight), I have decided to estimate a CATE function $\color{#7A28CB}\tau(o)$, which estimates the effect of my advertisement given a value $\color{#7A28CB}o$ of an indicator variable $\color{#7A28CB} O_i$ and is 1 if a consumer is under 21 and 0 otherwise. In formal notation, $\color{#7A28CB}\tau(o)$ can be written as.

$\textcolor{#7A28CB}{\tau(o)} = \mathbb{E}[\textcolor{#EF3E36}{P_i^1 - P_i^0}|\textcolor{#7A28CB}{O_i = o}]$

Suppose the table below presents 8 consumers whose data I received from Google Ads Platform in order to help me purchase ads that maximize the ROI of my marketing spend.

With this information, I can calculate a CATE conditional on two values $o = 0$ and $o = 1$ for $\color{#7A28CB}O_i$ by taking the mean of $\color{#7A28CB}P_1^1 - P_0^i$ for individuals under 21 as well as for individuals over 21. This calculation is as follows.

$\begin{aligned}\textcolor{#7A28CB}{\tau(1)} &= E[\textcolor{#EF3E36}{P_i^1}| \textcolor{#7A28CB}{o =1}] - E[\textcolor{#EF3E36}{P_i^0}| \textcolor{#7A28CB}{o =1}]\\&= \frac{1}{4}(1+1+1+1) - \frac{1}{4}(0+0+1+0) \\&= \frac{3}{4}\end{aligned}$

$\begin{aligned}\textcolor{#7A28CB}{\tau(0)} &= E[\textcolor{#EF3E36}{P_i^1}| \textcolor{#7A28CB}{u =0}] - E[\textcolor{#EF3E36}{P_i^0}| \textcolor{#7A28CB}{u =0}]\\&= \frac{1}{4}(1+0+0+0) - \frac{1}{4}(0+0+0+0) \\&= \frac{1}{4}\end{aligned}$

The results of these calculations can be interpreted as the following two english language statements.

• “Given that an individual consumer is over 21, exposure to my ad makes them 75% more likely to purchase a flight ticket from my brand.
• “Given that an individual consumer is not over 21, exposure to my ad makes them 25% more likely to purchase a flight ticket from my brand.”

Recall again from my previous blog post discussing the potential outcomes model that this calculation is unfortunately impossible as a result of the fundamental problem of causal inference, I cannot calculate $\color{#7A28CB}P_i^1 - P_i^0$ for all individuals $i$ as I only observe an observed outcome $\color{#7A28CB}P_i$ which equals $\color{#7A28CB}P_i^1$ if I expose individual $i$ to an ad and equals $\color{#7A28CB}P_i^0$ if I do not. Thus, I will need a methodology for estimating $\color{#7A28CB}P_i^1 - P_i^0$ from the $\color{#7A28CB}P_i$ I can observe utilizing data I am provided on observed individuals. What tools, algorithms, and procedures are commonly used to achieve a robust estimate of this value? More generally how can I estimate the expected value of a treatment effect $\color{#EF3E36}Y^1_i - Y^0_i$ given the value of a confounding variable $\textcolor{#7A28CB}{Z_i}$ in order to specify a CATE function $\textcolor{#7A28CB}{\tau(z)} = \mathbb{E}[\textcolor{#EF3E36}{Y_i^1 - Y_i^0}|\textcolor{#7A28CB}{Z_i = z}]$.

Estimating Conditional Average Treatment Effects

In order to estimate $\color{#EF3E36}Y^1_i - Y^0_i$ for an individual consumer an analyst will often leverage variation in the value of an explanatory variable $\color{#7A28CB}X_i$ of interest as is common with many causal inference methods. Particularly, an analyst will leverage variation in treatment within groups of observed individuals with similar values of confounding variables and will subsequently compare their outcomes. The hypothesis an analyst is leveraging is that when observed individuals have sufficiently similar values of confounding variables affecting their actions given treatment, their respective outcomes $\color{#EF3E36}Y^1$ and $\color{#EF3E36}Y^0$ are also very similar. For example, consider a group of two observed individuals $i$ and $j$ for which $i$ receives treatment and $j$ does not. Suppose that these individuals respective values of confounding variable $\color{#7A28CB}Z$, $\color{#7A28CB}Z_i$ and $\color{#7A28CB}Z_j$ are similar, and are both approximately equal to a particular value $z$ (which can be written mathematically as $\color{#7A28CB} Z_i \approx Z_j \approx z$), then $\color{#EF3E36} Y_i^1 \approx Y_j^0$ and $\color{#EF3E36} Y_i^1 \approx Y_j^1$. As a result, one can estimate $\color{#EF3E36}Y^1_i - Y^0_i$ for a particular observed individual conditional on a confounding variable with the value $\color{#7A28CB}z$ as follows.

$\begin{aligned}\textcolor{#7A28CB}{\tau(z)} &= E[\textcolor{#EF3E36}{Y_i^1}| \textcolor{#7A28CB}{Z_i =z}] - E[\textcolor{#EF3E36}{Y_i^0}| \textcolor{#7A28CB}{Z_i =z}]\\&\approx E[\textcolor{#EF3E36}{Y_i^1}| \textcolor{#7A28CB}{Z_i \approx z}] - E[\textcolor{#EF3E36}{Y_j^0}| \textcolor{#7A28CB}{Z_j \approx z}]\end{aligned}$

How can an analyst identify these groups? We’ve used $\approx$ to represent “similarity”, but mathematically, what exactly does that mean? What are the strategies we can use to enable us to make comparisons between “similar observed individuals?

Subclassification

One way an analyst can estimate conditional average treatment effects is subclassification, which splits observed individuals into subclassifications along variation in their respective values of confounding variables. For example, if an analyst wishes to understand the effect of their treatments on different genders, they may split their population of observed individuals by gender, and estimate causal effects within each defined gender. Once observed individuals have been split into subclassifications, an analyst can estimate causal effects within these groups by leveraging the simple difference in mean outcomes (SDO) calculation discussed in my post covering average treatment effect estimation. As the name suggests, leveraging the SDO requires an analyst to calculate the difference in the mean outcomes within each group with value $\color{#7A28CB} \approx z$ in order to estimate $\color{#7A28CB} \tau(z)$. An analyst can use this to estimate CATE as a result of a useful theorem from probability theory $E[A - B] = E[A] - E[B]$, and thus:

$\begin{aligned}\textcolor{#7A28CB}{\tau(z)} &= E[\textcolor{#EF3E36}{Y_i^1} - \textcolor{#EF3E36}{Y_i^0}| \textcolor{#7A28CB}{Z_i =z}]\\&= E[\textcolor{#EF3E36}{Y_i^1}| \textcolor{#7A28CB}{Z_i =z}] - E[\textcolor{#EF3E36}{Y_i^0}| \textcolor{#7A28CB}{Z_i =z}]\\&\approx E[\textcolor{#EF3E36}{Y_i^1}| \textcolor{#7A28CB}{Z_i \approx z}] - E[\textcolor{#EF3E36}{Y_j^0}| \textcolor{#7A28CB}{Z_j \approx z}]\end{aligned}$

For example, consider my digital advertising causal inference task analyzing which internet users are most susceptible to influence from my ads. Suppose I choose to complete analysis leveraging only an observed individual’s Age $\textcolor{#7A28CB}A$ which is provided to me as contextual information by Google Ads Platform. One way I could use sub-classification to identify groups of individuals with similar values for this confounding variable would be to split these individuals into sequenced age sub-classifications spanning 10 years. Once I have split these individuals into buckets, I can take the difference of the means of indicator variable Purchases Flight between treated and untreated individuals within each bucket in order to estimate a CATE function $\color{#7A28CB}\tau(a)$ conditional on the age of each observed individual. Mathematically, I am leveraging the following calculation to estimate the susceptibility of a particular user to advertising given their age.

$\begin{aligned}\textcolor{#7A28CB}{\tau(a)} &= E[\textcolor{#EF3E36}{P_i^1} - \textcolor{#EF3E36}{P_i^0}| \textcolor{#7A28CB}{A_i =a}]\\&= E[\textcolor{#EF3E36}{P_i^1}| \textcolor{#7A28CB}{A_i =a}] - E[\textcolor{#EF3E36}{P_i^0}| \textcolor{#7A28CB}{A_i =a}]\\&\approx E[\textcolor{#EF3E36}{P_i^1}| \textcolor{#7A28CB}{A_i \approx a}] - E[\textcolor{#EF3E36}{P_j^0}| \textcolor{#7A28CB}{A_j \approx a}]\end{aligned}$

An interactive visualization illustrating this subclassification process is presented below. The mean calculated for each subclassification represents the effect of my ad on a consumer conditional on their age, for example one could interpret a calculated mean of 0.4 for the 40-49 range as the following english language statement: “Given that a consumer is within the age range of 40 to 49, exposure to my ad will make them 40% more likely to purchase a flight ticket from my brand.”

Matching

Another way causal inference analysts try to identify groups of individuals exposed and unexposed to treatment with similar respective values of particular confounding variables is matching. Matching consists of selecting pairs of similar observed individuals, of which one is exposed to treatment and one is not. The “similarity” of these individuals in pairs can be measured in a variety of ways but this metric is generally calculated as the distance between the values of their confounding variables. Within these pairs, called matched samples, the values of confounding variables are approximately constant across individuals, and thus an analyst can estimate the extent of a treatment effect conditional on these confounding variables, by comparing the outcomes of each pair’s observed individual that is exposed to treatment and its observed individual that is not.

For example, if I am using matching to condition on a single confounding variable $\color{#7A28CB}Z$, by taking the mean of difference between the purchasing decisions between the similar individuals in each pair exposed and unexposed to treatment, I can calculate the following value

$\begin{aligned} \textcolor{#7A28CB}{\tau(z)} = E[\textcolor{#EF3E36}{Y_i^1}| \textcolor{#7A28CB}{Z_i \approx z}] - E[\textcolor{#EF3E36}{Y_j^0}| \textcolor{#7A28CB}{Z_j \approx z}]\end{aligned}$

and achieve an estimate of the conditional average treatment effect $\color{#7A28CB}\tau(z)$ at each values $\color{#7A28CB}z$ which corresponds to a match.

Consider the interactive visualization below displaying the matching process for my digital advertising causal inference task. At first this visualisation displays the same plot shown in figure 4, of 32 individuals plotted by their age as well as whether or not they purchase a flight. After pressing the “Match Observations” button, data points representing individuals with similar ages will match, represented by a migration to a plot of matched samples. I can compare these pairs of similar individuals to achieve an estimate of the effects my ads have on a particular consumer conditional on their age.

Bias In Estimation Of CATE

Much like any estimation of a causal effect, estimations of conditional average treatment effects are susceptible to distortions from confounding bias, which distorts the estimate of a causal effect by adding additional correlation between an explanatory variable and an outcome variable within a causal relationship of interest. Additionally recall from my confounding bias post that in order to achieve an unbiased estimate of a causal effect an analyst must estimate the extent of the effect while “conditioning” on all confounding variables. This is because treatment and potential outcomes of an observed individual are conditionally independent given these confounding variables, meaning that when these confounding variables are constant, there is no additional correlation distorting an analysts estimate of a causal effect.

When estimating a conditional average treatment effect, conditioning on confounding variables is rather straightforward, as conditioning on confounding variables is inherent to the estimation of this type of causal effect. In an ideal scenario, I am able to use matching or subclassification to estimate a CATE conditioning on each and every confounding variable which may affect the explanatory variable and outcome variable in my causal relationship of interest. In this scenario, an analyst doesn’t have to worry about confounding bias distorting their estimation and can confidently leverage their calculated estimate to inform future decisions. For example, if the confounding variables affecting both Exposed To Ad and Purchases Flight in my digital advertising causal inference task are Past Behavior, Demographic Data, and Psychographic Data, and I am sufficiently able to condition on these 3 variables using matching or sub-classification then my resultant estimate of the causal effect of Exposed To Ad on Purchases Flight conditioning on Past Behavior, Demographic Data, and Psychographic Data (represented mathematically as $\textcolor{#7A28CB}{\tau(b,d,s)} = \mathbb{E}[\textcolor{#EF3E36}{P_i^1 - P_i^0}|\textcolor{#7A28CB}{B_i = b,D_i=d,S_i=s}]$) should not be biased.

Of course, achieving an unbiased estimate of a conditional average treatment effect is only easy in an ideal scenario and analysts often seek to produce causal inference insights leveraging data which is less than ideal. The principal barrier to this ideal scenario is an upper limit on the number of confounding variables which can be effectively conditioned on. While an analyst might be tempted to condition their estimate on every possible confounding variable they can measure, an increase in the number of conditioned confounding variables (a value commonly referred to in causal inference literature as the dimensionality of analyzed data) diminishes the amount of observed individuals within each “similar” group identified with matching or subclassification. For example, the information provided by Past Behavior, Demographic Data, and Psychographic Data could comprise hundreds or even thousands of individual scalar values. While an analyst may be tempted to condition on all of these variables in order to ensure their estimate of CATE is unbiased, such an action would shrink the number of observed individuals which are similar enough to compare. This phenomenon is illustrated in the visualization below, explaining how conditioning on just one more variable can make subclassification more challenging for my digital advertising causal inference task.

Curse Of Dimensionality

The curse of dimensionality, is a causal inference paradox describing situations in which leveraging more information in an analysis can decrease the accuracy of a CATE estimate. In order to avoid this curse, an analyst will need to be clever about how they select the confounding variables they condition on when attempting to calculate an unbiased CATE estimation. In academic fields, such as economics, medicine, and epidemiology, analysts often rely on underlying theoretical concepts to inform the specification of a smaller causal graph and more easily estimate causal effects.

However, causal inference practitioners with access to more sophisticated tools can more effectively identify the confounding variables which would eliminate the greatest amount of confounding bias and select these for conditioning in conditional average treatment effect estimation. For example, for my digital advertising causal inference task, I may refrain from using industry expertise in marketing to try and intuit which confounding variables out of thousands I should condition my CATE estimates on in order to ensure by CATE estimation is optimally accurate. Perhaps, I would rather automatically identify the possible confounding variables which have the greatest effect on both Exposed To Ad and Purchases Flight . Leveraging a machine learning technique for this problem could save me valuable time I would otherwise spend analyzing game theoretic models or testing my ads in focus groups to identify this optimal set of confounding variables. A machine learning technique would also likely improve the accuracy of my estimate; regardless of how good I am at understanding underlying mechanisms which drive a consumer’s engagement with my brand, a machine learning strategy for solving this problem will likely be able to complete this task with much more scientific rigor.

Lifting The Curse

What machine learning strategies exist for selecting the optimal set of confounding variables for an analyst to condition their CATE estimates on? What is the evaluation metric for such strategies? For example, how would such a strategy identify which confounding variables have the greatest effect on Exposed To Ad and Purchases Flight? All this and more will be revealed in my next blog post! (You can subscribe to receive email updates here).